This article is the fifth in a series of insights into the more purely technical part of Bitcoin, accessible even to those who are not familiar with coding.
This article is also a sort of guide designed to gradually go down what many call “the rabbit hole”.
In terms of books, it is necessary to mention “Mastering Bitcoin” by Andreas Antonopoulos, a regular reference, from which the images in this article were taken.
Introduction
First, it is necessary to define bitcoin and Bitcoin as:
- bitcoin (in lowercase as a unit of account): the first digital, transferable, non-duplicable, decentralised asset;
- Bitcoin (in uppercase as a value transfer system): a protocol that generates a peer-to-peer network that allows each node that composes it to transact value freely and in a pseudonymous way to other nodes in the network. This value, or more correctly, digital representation of value, is generated by the protocol in order to ensure scarcity, security in the order of transactions and security of the system itself.
The system and its native unit of account were made possible, in Andreas Antonopoulos’ vision, by four key innovations, resulting from decades of research in the fields of cryptography and distributed systems, brought together in one powerful solution:
- a decentralised peer-to-peer network (the Bitcoin protocol, although this term can be used to refer widely to all four points);
- a ledger of public transactions (the blockchain);
- the issuance of a decentralised, mathematical and deterministic currency (distributed mining);
- a decentralised transaction verification system (the transaction script).
Joining the system using the native unit of account is simple, it is enough to download a wallet application (for pc, tablet, smartphone, smartwatch, etc.) or use a web application. The three main forms of the Bitcoin client are:
- full client, or “full node”, a client that keeps a complete copy of the blockchain, manages the user wallets (and initially managed mining);
- light client, or “light node”, which records the user wallet but relies on third-party servers to access the network;
- web client, which is accessed via a web browser and which stores user data on a third-party server (not to be confused with applications such as Coinbase).
During the following paragraphs, it should be noted that the changes made by SegWit, to which a specific section will be dedicated, have not been dealt with.
Keys and addresses
Keys
The ownership of bitcoins is determined by:
- digital keys;
- bitcoin addresses;
- digital signatures.
Keys are not stored on the network, but by users in the wallet (files or databases for creating and storing keys). These are key pairs consisting of a private key and a public key. The only representation of the keys that users see is the bitcoin address, usually (but not exclusively) generated by and corresponding to a public key. Bitcoin uses the elliptical curve multiplication as the basis for its public key encryption: the key pair consists of a private key (to spend bitcoin) and a single public key (to receive bitcoin) that derives from the private one. The mathematical relationship between the two keys allows the private one to be used to generate signatures on messages, and the public one to validate this signature without revealing the private key.
A wallet contains a collection of key pairs, where:
- the private key (k) is a number (usually chosen at random before the advent of deterministic wallets, which now constitute the best solution and will be discussed in further detail);
- a public key (K) is generated by k through elliptical curve multiplication (a unidirectional cryptography function);
- a bitcoin address (A) is generated by K through a hashing algorithm (a one-way encryption function).
Private keys. A private key is a random number, which must not be revealed under any circumstances (or lost, otherwise the associated bitcoins will be lost), ergo the safest way to generate a private key is to find a source of entropy or randomness. The bitcoin client uses the random number generator of the OS (usually initialised by a source of randomness – in the case of deterministic HD wallets the generator is used to create the seed from which the keys are generated) to produce 256 bits of entropy. The private key could be any number between 1 and n-1, where n is a constant (1,158 * 1077 a little less than 2256) defined as the order of the bitcoin elliptical curve. When a 256-bit random number is generated (usually by submitting a longer string of random bits to the SHA256 hash algorithm), if the result is less than n-1 the key is adequate.
The following is a randomly generated private key (k) shown in its hexadecimal representation (256 digits shown as 64 hexadecimal digits, each with 4 bits):
1E99423A4AND27608A15A2616A2B0E9AND52CEDED330AC530ANDCC32C8FFC6A526AEDD
Public keys. The public key is generated from the private key through the elliptical curve multiplication, irreversible, K = k * G where:
- k is the private key;
- G is a constant called a generator point.
The reverse operation, known as “finding the discrete logarithm”, calculating k knowing K has the same difficulty as finding the value of k through a brute-force attack.
Bitcoin uses a specific elliptical curve and a set of mathematical constants, defined in a standard called secp256k1, established by the National Institute of Standards and Technology (NIST).
Starting with a private key k, and multiplying it by a predetermined point of the curve called the generator point G, another point on the curve is produced, which corresponds to the public key K. The generator point G is specified as part of the standard secp256k1 and in bitcoin, it is the same for all keys, ergo a private key k multiplied by G will always result in the same public key K. The relationship between k and K is fixed, but can only be calculated in one direction, from k to K.
When implementing the elliptical curve multiplication, the k shown above is taken and multiplied by G in order to obtain K:
K = 1E99423A4AND27608A15A2616A2B0AND9AND52CEDED330AC530ANDCC32C8FFC6A526AEDD * G
The public key is defined by the coordinates of point K = (x, y):
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
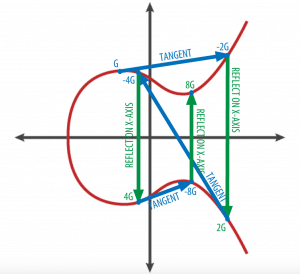
To display the multiplication of a point with an integer, the simplest elliptical curve is used with respect to the real numbers (the mathematics is the same). The goal is to find kG, multiple of G, which is equivalent to adding G to itself, k times in a row. In elliptical curves, adding a point to itself is equivalent to drawing a tangent on the curve at the point and finding where it intersects the curve again, then reflecting that point with respect to the x-axis.
Addresses
Addresses produced by public keys consist of a string of numbers and letters and start with 1 (until SegWit is activated), here is an example: 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
The bitcoin address is where the value is sent within a transaction. A bitcoin address can represent:
- The owner of a private/public key pair;
- A payment script.
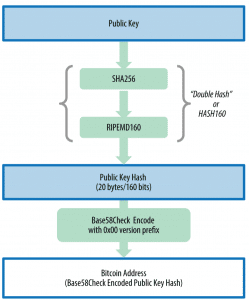
Previously it has been said that a bitcoin address (A) is generated from K through a hashing algorithm (a unidirectional cryptography function). A “hashing algorithm” is a unidirectional function that produces a digital fingerprint (digest or code) or “hash” of an input of arbitrary size. These functions are fundamental in Bitcoin and are present in different parts of the system. The algorithms used to create a bitcoin address from a public key are Secure Hash Algorithm (SHA) and RACE Integrity Primitives Evaluation Message Digest (RIPEMD), in particular, SHA256 and RIPEMD160. From the public key K it is calculated first the hash SHA256 and then the hash RIPEMD160, generating a 160-bit number (20-byte).
Bitcoin addresses are almost always presented in an encoding called Base58Check, which uses 58 characters (a system of Base58 numbers) and a checksum (bech32 will be explored later) to avoid ambiguity and protect against errors in the transcription and recording of addresses.
Private key formats. Private keys can be represented in different formats, which correspond to the same 256-bit number. Hexadecimal and raw binary are used internally in software and rarely shown to users, while WIF is used for the import/export of keys and often used in a QR code representation (barcode). The BIP 38 standard allows for the encryption of private keys (compatible with several Bitcoin wallets and clients) with a passphrase and the encoding of them with Base58Check so that they can be stored securely on backup devices, transported securely between wallets or stored in any other condition in which the key may be exposed. The encryption standard uses the Advanced Encryption Standard (AES), a standard established by the National Institute of Standards and Technology (NIST) and widely used in data encryption implementations for commercial and military applications. A BIP0038 encryption scheme accepts as input a bitcoin private key, usually encoded in WIF, such as a Base58Check string-type with a prefix “5” (for public keys that are not compressed, while those used for years were compressed public keys, indicated by private keys that start with “L” or “K”). In addition, the BIP0038 encryption scheme accepts a passphrase, a long password, usually composed of several words or a complex string of alphanumeric characters. The result of the BIP0038 encryption scheme is an encrypted private key with Base58Check encryption starting with the prefix 6P.
Pay-to-Script Hash (P2SH) and Multisig addresses. Bitcoin addresses starting with number 3 are pay-to-script hash addresses (BIP 16). They define the recipient of a bitcoin transaction as a script hash instead of the owner of a public key. Unlike transactions that allocate funds to traditional bitcoin 1 addresses (hash pay-to-public-key or P2PKH), funds sent to addresses 3 require more than submitting a public key hash and private key signature as proof of ownership. Requirements are defined when the address is created, within the script, and all inputs to this address will be “cluttered” with the same requirements. A pay-to-script hash address is created with a transaction script (which defines who can spend the UTXO). The encoding of a P2SH address is done through the same double-hash function used during the creation of a bitcoin address, applied only on the script rather than on the public key: script hash = RIPEMD160 (SHA256 (script))
The resulting hash script is encoded with Base58Check using the version 5 prefix, resulting in an encoded address starting with 3. An example of a P2SH address is 32M8andnmuyZ2zVbes4puqe44NZumgG92sM
The most common implementation of the P2SH function is the multi-sig (multi-signature) script address. The script requires more than one signature to prove the property (ergo spend the UTXO). The Bitcoin multi-sig functionality is designed to require M signatures (also known as “thresholds”) from a total of N keys, known as M-on-N multi-sig, where M is equal to or less than N.
Vanity addresses
These are custom-made Bitcoin addresses that can be read by humans, such as 1LoveBPzzD72PUXLzCkYAtGFYmK5vYNR33 which contains the letters that form the word “Love” as the first four letters Base-58. Creating a vanity address requires testing billions of private keys until the resulting address has the desired characteristics. The process is mere repetition (brute-force): select a private key at random, derive the public key, derive the address and check whether the result meets the conditions. Like any other address, a vanity depends on the same Elliptic Curve Cryptography (ECC) and Secure Hash Algorithm (SHA).




