To date, there are several cryptocurrencies whose mining is based on different mechanisms of Proof of Work for the verification and validation of blocks that are inserted in the blockchain.
Such PoWs are often based on different algorithms and hashing functions.
There are several of them. Among them the most famous is the SHA-256, mainly used for mining Bitcoin and its fork Bitcoin Cash. Then there is Scrypt, used by Litecoin and also by the entertaining DOGE.
Another famous algorithm is the CryptoNight, used by Monero and dozens of different altcoins. Then there’s Ethash, used by Ethereum and Ethereum Classic. Finally, DASH uses the efficient X11. There are many other PoWs, but this first article will deal only with the most popular.
SHA-256
The SHA-256, acronym for Secure Hash Algorithm, in this case with a 256-bit digest, belongs to a set of cryptographic functions and was the first to be used in the cryptocurrency world.
Like any hash algorithm, the SHA-256 produces a message digest from a message of variable length. This does not allow tracing back to the original message knowing only the latter, as the function is not reversible. In addition, this mechanism also makes it possible to prevent the intentional creation of two different messages with the same digest.
The hashing function of the SHA-256 is not particularly complex, so it doesn’t require a lot of resources to execute it. In fact, the function uses simple logical and arithmetic operations, without the need to use fast memories and special instructions, which is why the function can be easily implemented on FPGAs or in the layout of specially designed chips, i.e. ASICs.
ASICs are far more efficient and have a greater hashrate than GPUs and CPUs, as they can only perform the function for which they were designed, in this case the SHA-256 hashing function. Generally, ASIC throughput on SHA-256 algorithms is now measured in Th/s.
How the SHA-256 algorithm works
Redundant bits are added to the original message so that the final length of the message is consistent with 448 modulo 512 (famous MD5). The modulo is nothing more than a function that has as a result the remainder of the division between the two numbers when it is possible to execute it. In this case, 448 modulo 512 is equivalent to 448 bits. In this way, the length of the “message+padding” is equal to a number of 64 bits smaller than a multiple of 512 bits.
Next, a 64-bit integer containing the length of the original message is added to the newly created bit sequence. At the end a sequence of bits will be obtained which is a multiple of 512.
The third step is to initialise the MD buffer. It is a 256-bit buffer divided into eight registers of 32 bits each. The eight registers will be conventionally indicated with (A, B, C, D, E, F, G and H) and initialised with a series of hexadecimal values.

Finally, there is the actual processing of the 512-bit blocks. The previously generated “message+padding+messageLength” bit sequence is divided into blocks of 512 bits. These blocks are identified with Bn, with n ranging from 0 to N.
The core of the SHA algorithm is called compression function and consists of 4 cycles of 20 steps each. Cycles have a very similar structure to each other except for the fact that they use a different primitive logic function.
Each block is taken as input parameter by all 4 cycles together with a constant K and the values of the eight registers. When the computation is over, new values will be obtained for A, B, C, D, E, F, G, H, which will be used for the computation of the next block until the final block H is reached.
Scrypt
To combat ASICs and therefore the danger of “centralisation of computing power”, another mining algorithm was developed, which was then implemented in the Proof of Work protocols of some cryptocurrencies. Scrypt, which is the name of the algorithm, uses some functions that make extensive use of memory to drastically reduce the efficiency of logic circuits typical of ASICs. However, to make the use of Scrypt fast and efficient even on common PCs, some parameters were simplified with very bad consequences.
The algorithm initially, had CPU mining as its only objective. However, shortly after the debut came the first software tools for GPU mining. A year later, towards the end of 2013, the first Scrypt based ASICs arrived, decreeing the failure of the objectives set by this algorithm.
When mining with high-performance computers or ASICs, throughput is generally measured in Kh/s or at most Mh/s.
How the Scrypt algorithm works
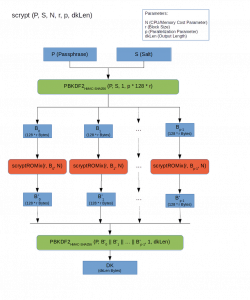
The Scrypt algorithm has several parameters, including N, which defines the cost in terms of resources involved in executing the algorithm. Then there is the parameter p, which defines the parallelisation, and r, which defines the size of the blocks and therefore the memory used. There are also other parameters related to the hash function and the length of the output hash.
The operation of the Scrypt has two initial parameters, namely the message to be encrypted and the Salt, a random string used to add entropy and defend the system from attacks based on precomputed Rainbow tables. They are nothing more than association tables that offer a time-memory compromise for the recovery of clear encryption keys from hashed keys.
The data is then fed to a special key derivation function, PBKDF2, which stands for Password-Based Key Derivation Function 2. This function, using the parameters previously dictated by the algorithm, further reduces the vulnerabilities of the encrypted key to brute force attacks. The PBKDF2 generates a number p of 128*r Bytes blocks [B0…Bp−1].
At this point, using the ROMix function, in this case of sequential memory-hard type, the blocks are mixed, even in parallel. The output mixed blocks are then passed as a Salt parameter (expensive Salt) to another PBKDF2 that generates a key of the desired length.
CryptoNight
The CryptoNight is used to mine those coins featuring the CryptoNote protocol, including Monero. It is a function strictly bound to the memory (memory hard hash), in this case to the third level Cache memory of the CPUs as it is focused on the latency. This constraint was imposed to make the CryptoNight inefficient on systems such as GPUs and FPGAs, but especially ASICs, not equipped with cache memory and therefore disadvantaged or virtually impossible to use the algorithm.
The Proof of Work CryptoNight algorithm first initialises a Scratchpad, i.e. a memory area used to store the data used. In the case of CryptoNight, pseudo-random data is used specifically to inhibit its use by ASICs and to minimise GPU efficiency. The algorithm also performs numerous read and write operations on the scratchpad to emphasize the speed of the memory and bring out the latency, which must be as low as possible. Finally, using the data in the scratchpad and a hashing function, an appropriate value is produced.
The size of the CryptoNight scratchpad is about 2 MB of memory for each instance due to the following reasons:
- can be contained in the L3 caches (per core) of modern processors;
- an internal memory of a megabyte is (or rather was) an unacceptable size for the ASIC pipeline;
- GPUs can run tens or hundreds of threads but will be limited by GDDR5 memory, with a much worse latency than the L3 cache of modern CPUs;
- a significant expansion of the scratchpad would require an increase in interactions. This would imply an increase in the time required. Continuous and prolonged calls to the p2p network could therefore compromise the network and lead to some vulnerabilities, as the nodes are obliged to perform a PoW check of each block. If a node spent a considerable amount of time on the hash of a block, it could easily be flooded with a false block flooding mechanism causing a DDoS.
The CryptoNight remained untouched by the ASICs for several years, until Bitmain, Baikal and Halong Mining announced several models of the CryptoNight ASICs on March 15th, 2018, capable of returning hashrates above 200 KH/s.
Since then, Monero’s team has repeatedly acted on CryptoNight parameters, making the Proof of Work even more memory-constrained.
How the CryptoNight algorithm works
Hash input is initialised using the Keccak (SHA3 function), with parameters B equal to 1600 and C equal to 512. The final parameters of the Keccak, i.e. the Bytes from 0 to 31, are interpreted as an AES 256 key and expanded in 10 round keys.
Bytes between the 64th and 191st are extracted in eight blocks of 16 Bytes each, which are then encrypted. Everything is then allocated in the scratchpad, which has a size close to 2 MB, as previously described.
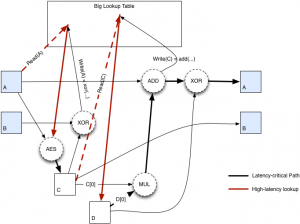
Once this is done, an XOR is imposed among the first 63 Bytes of the Keccak to initialise the A and B constraints, each of 32 Bytes. These variables and their processing are used to impose a loop of continuous readings and writings (524288 times) in the scratchpad, so that the algorithm is strictly bound to the latency of the memory. Finally, the final hash sequence of the previously obtained data is calculated.
Ethash
Ethash, as the name suggests, was created as a function to perform the Proof of Work of the Ethereum blockchain. This algorithm mixes two standard cryptographic functions, the SHA-3 and the Keccak. This results in a function that is resistant to ASICs but at the same time fast to verify and execute.
The resistance to ASICs is guaranteed by the memory-hard nature of the algorithm, given the use of a pseudo random data set initialised according to the length of the blockchain, therefore variable. This data set is called DAG (directed acyclic graph) and is regenerated every 30 thousand blocks (about 5 days).
Despite this, on April 3rd, 2018, Bitmain announced the long-awaited Antminer E3, the first ASIC for Ethash capable of delivering a hashrate of about 200 MH/s with an absorption of almost 800 Watts.
Currently the DAG has a size of about 3.4 GB, which is why it is not possible to mine Ethereum with video cards with less than 3GB of video memory, as the data set is necessary for the operation of the hash function.
In the case of mining performed with high-performance computers, throughput is generally measured in Mh/s or at the most Gh/s.
How the Ethash algorithm works
First, a pre-processed header from the last block and the current Nonce, i.e. a random 32-bit number generated by the miners as a hash target, are combined together using the SHA-3. A 128 byte long mixed byte sequence, called Mix 0, is then created.
The Mix is used to determine which data to collect from the DAG, using a special fetch function. Subsequently, the Mix 0 and the data recovered from the DAG are mixed, generating a new string of 128 Bytes, called Mix 1. This operation is performed with the same procedure 64 times, until the last string, that is the Mix 64, is reached.
The Mix 64 is then processed into a 32-byte sequence called the Mix Digest. This sequence is then compared with a second target sequence. If it is less than the target, then the Nonce is considered reached and the broadcasting to the Ethereum network begins. Otherwise, the algorithm is re-executed with a new Nonce.
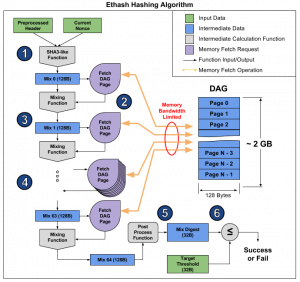
The constraint that makes the algorithm closely related to memory and to the bandwidth in particular, therefore also the bus, consists in the access to the DAG to fetch the data.
X11
The X11, successor of the X13, X15 and X17 variants, is a Proof of Work algorithm designed to be very efficient on both CPUs and GPUs. As the name suggests, it uses a combination of eleven different encryption algorithms.
Unfortunately, the X11 did not prove to be ASIC Proof, as after a few months the first ASICs dedicated to this algorithm were made available.
Unfortunately, there are not many technical details about how X11 works, except for the names of the eleven hashing algorithms used: blake, bmw, groestl, jh, keccak, skein, luffa, cubehash, shavite, simd, echo. The combined use of these hash functions allows a high level of safety to be achieved while maintaining an efficiency 30% higher than the classic SHA-256.



