In this section, we will analyse the functioning of some of the mining algorithms (Proof of Work) used by some altcoins. More specifically, the ones to be examined include Equihash, used by ZCash, and Blake2b, currently used by SiaCoin.
Other Proof of Work algorithms discussed include the latest X16R and X16S, used by RavenCoin and PigeonCoin, followed by Tensority, used by Bytom.
There is also another in-depth analysis of the main mining algorithms used by the most famous coins.
Proof of Work algorithms: Blake2b, Equihash, Tensority and X16R & S
Blake2b
The Blake2b is a version derived from the Blake2. Blake2 is a cryptographic hashing function, i.e. it produces a fixed-length message digest from a variable-length message.
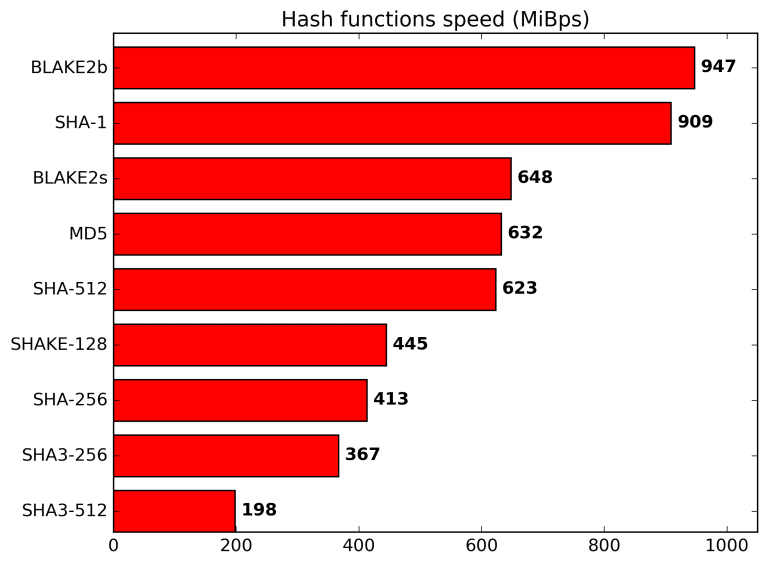
This does not allow recovering the original message knowing only the latter one, as the function is irreversible. Specifically, the Blake2 is faster than many other hashing functions, particularly the MD5, SHA-1, SHA-2 and SHA-3, as can be seen in the chart below. Nevertheless, it still allows maintaining a high level of security, equal to the latest SHA-3 standard.
The Blake2 function is completely open-source and the sources are available on the homonymous GitHub repository. The Blake2 has two variants:
- The Blake2b (or simply Blake2) is the version optimised for 64-bit platforms, including ARM processors, and produces digests of any size between 1 and 64 bytes;
- The Blake2s, on the other hand, is optimised for 8 to 32-bit platforms and produces digests of any size between 1 and 32 bytes;
- The Blake2x can produce digests of arbitrary length.
The algorithm is also able to take full advantage of multi-core, as it takes advantage of the SIMD instructions of modern CPUs. More specifically, there are two specific versions designed for 4-way and 8-way parallel execution, respectively the Blake2bp and Blake2sp.
There are also other Blake derivations used in mining, in particular, the Blake256R14 and the Blake256R8, which are almost the same but with a different message digest size.
Operation of the Blake2b algorithm
Blake2 is actually a refined and therefore improved version of Blake. Compared to the latter, in fact, it removes the addition of constants to the words of the message in the Round Function of the Blake, changes two rotation constants and simplifies padding.
An XOR is then added between a block of parameters and the initialisation vectors, and finally, the number of rounds is reduced from 16 to 12 for Blake2b and from 14 to 10 for Blake2s, in order to significantly speed up the hashing operation.
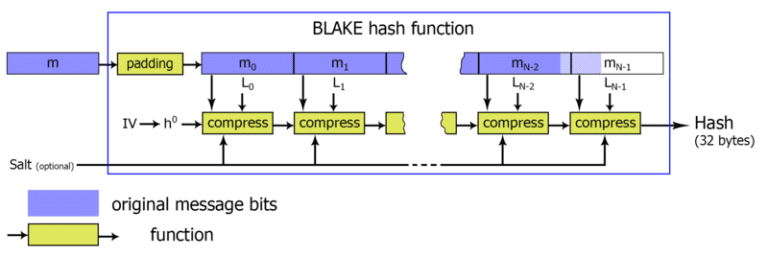
The first operation consists in initialising the state vectors (h) starting from the eight initialisation vectors (IV0 to IV7). Subsequently, h0 is calculated, which will be fed to the actual compression function. This last function will calculate 16 local vectors, the first 8 starting from the state vectors (h) and the other 8 using the IV initialisation vectors.
At this point, a mixing operation is carried out between the state vectors and two groups of 8 bytes coming directly from the input message m. The mixing function simply performs XOR operations, permutations and sums between the state vectors and the 8 bytes of the message.
In the case of blake2b, the mixing operation is carried out for 12 rounds. In the end, a 64-byte hash is obtained.
Equihash
Equihash is an asymmetric Proof of Work mechanism that is memory-hard, as it requires a lot of memory to generate an instant verification test. This constraint has kept the algorithm ASIC Proof for a long time, but last year Bitmain announced a specific model for Equihash-based coins.
The essence of the Equihash algorithm is based on the generalised birthday problem and Wagner’s enhanced resolution algorithm. To make the function difficult to implement on ASICs and hence mainly usable on CPUs and GPUs, Equihash implements a system of time and memory constraints, so as to penalise the calculation on those devices with little memory. On the other hand, however, since it is asymmetrical and with a few sequential steps, Equihash can be easily parallelised.
Operation of the Equihash algorithm
It’s a bit difficult to explain how Equihash works. First, two parameters must be defined, n and k, which are necessary for the Equihash solver. These parameters must be chosen carefully because they have an impact on the resolution efficiency of the algorithm.
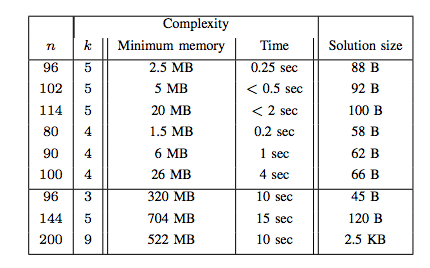
In the case of ZCash, n=200 and k=9 are used as parameters, as they have been found to be the most efficient parameters to use, both in terms of memory used and processing time.
After setting the parameters, the generalised birthday problem is resolved. The latter consists in finding a series of values x1, x2, …, x2k, all less than 2n/(k+1)+1, such that the operation XOR among the corresponding hash values calculated through a Blake2b hashing function, is equal to zero. Analytically speaking, therefore, the result will be:
H(x1) xor H(x2) xor …xor H( x2k) = 0 where H is the Blake2b hashing function
It is precisely Wagner’s algorithm that allows solving this problem of sizing. Wagner’s algorithm requires a quantity of memory equal to O(2n/(k+1)), thus depending on the parameters n and k as mentioned before. Once these parameters are set, the reduction in available memory dramatically increases the execution time, which is why Equihash is bound to memory.
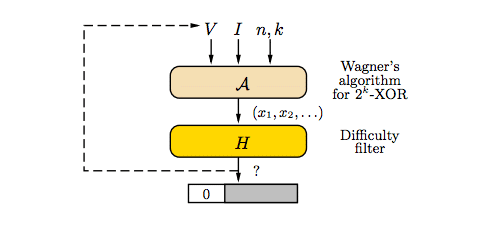
Rather than the amount of memory itself (about one Gigabyte, depending on the mining software, should suffice), the performance constraint is due to bandwidth, although this does not always affect significantly the mining performance, because a lot depends on the parameters chosen.
Tensority
Tensority is a fairly recent Proof of Work consensus algorithm, within which the use of matrices and tensors has been introduced, so as to exploit the mining power not only for hashing but also for the acceleration of Artificial Intelligence and for distributed parallel computing.
Tensority debuted on the Bytom coin. It’s an ASIC friendly algorithm, to the extent that Bitmain has announced practically at day-one the ASIC Antminer B3, dedicated exclusively to the mining of Bytom and probably characterised by the new chips intended for deep learning and artificial intelligence.
Tensority’s goal is to provide a new consensus mechanism for the blockchain and at the same time create a distributed network for deep learning and artificial intelligence services, so as to use this computing power in a useful and efficient way.
Operation of the Tensority algorithm
Tensority uses the Seed parameters and the hash of the block header as input. The seed is an array of 32 bytes determined by a certain period of life of the blockchain. It can, therefore, be considered as a snapshot of the history of consensus on the network. To obtain a validated block, miners will have to continue generating a nonce until it meets the difficulty requirement.
Tensority consists of five steps: the calculation of the cache, the construction of the matrix, the operations between matrices, the generation and validation of the work.
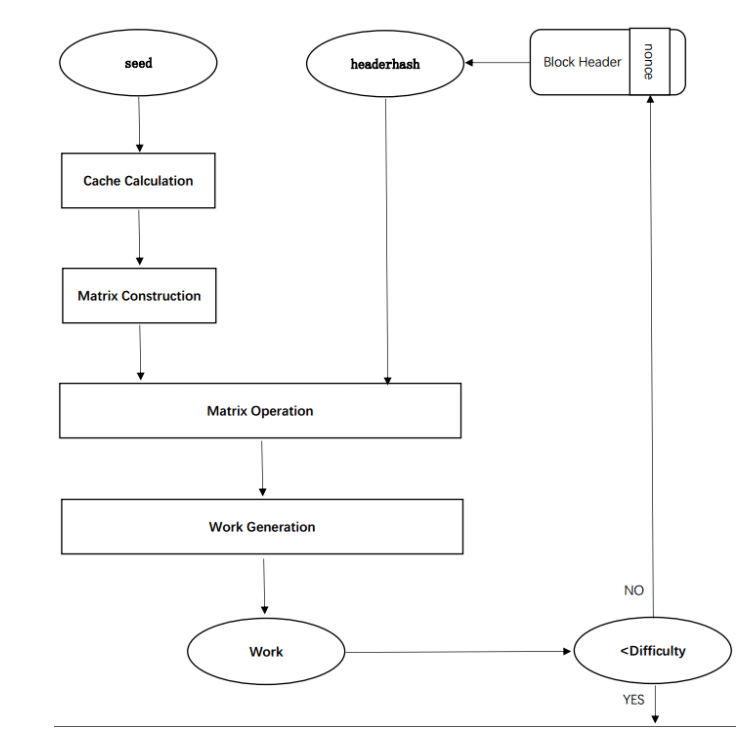
The cache is generated from the seed, because, compared to the block creation rate, the seed renewal occurs more slowly. Thus, the cache generated by the seed can be reused for a certain period of time.
Then we have the most innovative part of the algorithm, that is the construction of the matrix. This matrix is built by performing a series of operations of partitioning and grouping the cache.
After that, the next step involves operations between matrices. The number of operations that can be performed depends mainly on the miner’s computing power. Moreover, instead of the classic integer matrices, float64 are used, in order to support the operations carried out by the artificial intelligence algorithms, mainly based on float64. Finally, a hashmatrix is also generated.
At this point there is the actual PoW, which consists, starting from the hashmatrix generated at the previous step, of a 32-byte hash. Finally, a comparison is made between the value of the PoW performed and the difficulty of the block. If the work has a lower value, it can be considered valid and is therefore propagated to other miners. Otherwise, the miner will continue to redo the procedure using a different nonce until they receive a new validated block.
X16R & X16s
Finally, there are two fairly recent mining algorithms which are also ASIC Resistant, namely X16R and the X16s derivative. X16R was created with the aim of proposing a Proof of Work mechanism aimed at countering ASICs and making their development really unattractive. It is currently used by the currency RavenCoin.
The CryptoNight, Ethash and Equihash mining algorithms are memory-hard and are therefore heavily dependent on memory. The most recent X11, X13 and X15, on the other hand, consist of a sequence of hashing algorithms where the output of one becomes the input of the next. However, these approaches were not immune to ASICs.
X16R takes the approach of the X11/13 mining algorithms etc, but unlike the latter, it does not use a fixed sequence of use of the various algorithms. They are chosen randomly. The hashing algorithms used are the same as those used by the X15, to which a final hashing is added via the SHA512. However, the order of execution and which algorithms are executed is modified and chosen based on the hash of the previous block, in particular, the last 8 bytes.
This does not make it impossible to build an ASIC but requires the support of additional input for processing, currently easier to implement on CPUs and GPUs. Random reordering also prevents reusing the ASICs available for the X11 and X15.
The X16R hashing algorithm consists of 16 hashing algorithms operating in a random sequence, the sorting of which depends on the last 8 bytes of the previous block’s hash. The algorithms used are as follows:
- 0=blake
- 1=bmw
- 2=groestl
- 3=jh
- 4=keccak
- 5=skein
- 6=luffa
- 7=cubehash
- 8=shavite
- 9=simd
- A=echo
- B=hamsi
- C=fugue
- D=shabal
- E=whirlpool
- F=sha512
The PoW X16S variant
The X16S (Shuffle) is a variant of the X16R. Unlike the latter, the new X16S algorithm provides some hashrate stability and computational power utilisation. It can, therefore, be considered a kind of improvement, especially for miners. It is currently used by the Pigeoncoin coin, which can only be mined via CPU and GPU.
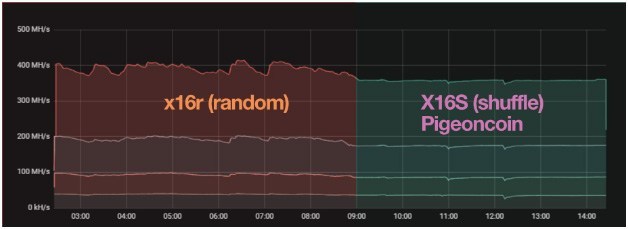
With X16R, in fact, choosing the algorithms to be executed randomly based on the hash of a previous block may lead to the same hash function being executed several times instead of performing them all. Since some hashing functions are more expensive than others, we get highly variable hashrates and power consumption. As a result, mining performance can be irregular, with all the possible consequences.
The Proof of Work X16S algorithm uses the last sixteen digits of the previous block to reorder a list containing all the hashing functions to be performed. X16S recreates the list using the value of each digit present in the last sixteen digits, so as to create an index within the list containing all the algorithms.
In summary, X16S randomises the order based on the hash of the previous block, but unlike X16R no algorithm is repeated or omitted. This allows all the advantages of the X16R to be exploited, significantly improving hashrate and stability.



